Already 2010 is feeling like the year of optimization. Everywhere I look, I’m seeing conversations about A|B and MVT testing, optimizing conversion flows, and understanding statistical significance.
When I first started running A|B tests, everything I did was on faith. I had good intention, I measured all the key indicators, but I had no idea how to tackle the question of “yeah but, is it statistically significant?” Then I began to crawl as I experimented with online calculators and eventually I moved on to building out my own formulas in Excel but still there was little confidence in myself, let alone the test results.
Eventually I began to experiment with testing tools like Google Web Optimizer, Amadesa, and Omiture Test & Target. This seemed to make life so much simpler as all the questions I was being asked were answered right in the testing application. Is it significant? Amadesa says they are 98% confident in the results. What is the lift we are seeing? Google Web Optimizer says its 8.5% and as a bonus it gives the confidence interval.
While I think it is extremely valuable to have your testing and optimization platform provide the key statistical measures that relate to your test, I think it is just as important to understand the math behind the reports, after all, you can’t call yourself a “car guy” or a “car girl” if you drive on the gauges alone and you don’t understand how the underlying systems work.
Let’s walk through an example campaign to understand how Omniture Test & Target calculates the statistics behind the results.
For our campaign, lets assume the following facts:
- Our campaign has two treatments, a control and one alternative.
- The control has had 4,008 visitors
- The alternative has had 4,003 visitors
- The control has had 377 conversions
- The alternative has had 355 conversions
#1 – Conversion Rate
Conversion rate equals the number of conversions divided by the number of starts, in this example we are using visitors but this can be visits, impressions, unique starts, etc. depending on how you measure site conversion.
Conversion Rate (control) = 377 / 4,008 = 9.41%
Conversion Rate (alternative) = 355 / 4003 = 8.87%
#2 – Standard Deviation
Standard Deviation shows how much variation (measures the spread or dispersion of a set of data) there is from the “average” (mean). As conversion rate is a binomial distribution, either a visitor converts or does not convert, the binomial distribution for variance is used:
Variance (control) = .0941(1 – .0941) = 0.09
Variance (alternative) .0887(1 – .0887) = 0.08
To calculate Standard Deviation from the variance, we take the square root of the variance:
Standard Deviation (control) = SQRT(0.09) = 0.29
Standard Deviation (alternative) = SQRT(0.08) = 0.28
#3 – Standard Error
The Standard Error is the estimated Standard Deviation of the error; the “noise” in the result. The Standard Error is calculated in order to calculate to Signal-to-Noise ratio.
To calculate the Standard Error for the Control:
Standard Error (control) = SQRT(0.09 / 4008) = 0.005
To calculate the Standard Error for the alternative:
Standard Error (alternative) = SQRT((0.09 / 4008) + (0.08 / 4003)) = 0.006
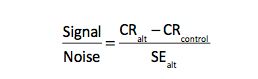
# 4 – Signal-to-Noise Ratio
To calculate the Signal-to-Noise ratio:
Signal-to-Noise = (9.41 – 8.87) / 0.006 = 0.84
OK….stay with me…..we are almost there.
#5 Finally We Arrive At Confidence
We will make use of the Signal-to-Noise ratio to calculate confidence using the Student’s T-Test.
Student’s T-Test = 1 – TDIST(ABS(0.84),(4003 + 4008 -2),2) = 0.60
As reported by Test & Target, we are 60% confident in the current results.
Extra Credit: Confidence Intervals
The Confidence Interval shows how much your test results can vary and still be within a predetermined confidence level. Standard confidence levels are 90%, 95%, 99%, and 99.5%. Omniture Test & Target uses the 95% confidence level.
To calculate the Confidence Interval:
Confidence Interval = 1.96(0.28 / SQRT(4003)) = 0.008
1.96 is a constant in this formula. 1.96 is equal to z*, which is taken from a Standard Normal Critical Values table based on 95% Confidence Level. The Standard Normal Critical Values Table can be found in any introductory level statistics book.
The formulas in this post have been provided by Omniture consulting. The screenshots have been taken from Omniture Test & Target and have been modified for the purpose of this example.

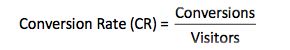



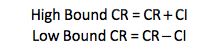
Thanks for posting this, well-written!
We work with GWO, Omniture and other testing tools and we often get asked about the math behind the results, so this is a very useful blog post.
(BTW, I really like your comment “you can’t call yourself a “car guy” or a “car girl” if you drive on the gauges alone and you don’t understand how the underlying systems work”.)
Interesting. This article is 100% lifted from the document that Test&Target consulting provides to customers.
You should at least credit the source before you paste the screenshots.
For some reason, you failed to provide a working email address so I’ll address your comment here. I have taken your advice and credited Omniture for the screenshots and the formulas. My intention was not to simply regurgitate the information provided by Omniture, which from my experience was extremely difficult to obtain and was incomplete, but to provide much needed clarity. My aim was to provide a working example to better understand the math behind the reporting and to answer why certain measures were used, for example the z* metric.
I also wanted to start a conversation around statistical significance in general. This IS the formula Omniture Test & Target uses, why would it be any thing else? But is it the right formula? Other testing tools use other approaches and online calculators differ as well. After reviewing the formulas with people who have a background in statistics, they have questioned if using the Student’s T-Test is the right way to do this or not.
Thanks again for your feedback and in the future, please leave a way to contact you.
how do you increase the confidence level in a test? do you do this by increasing traffic to each group (in your example visitors) or are there other ways?
From my experience, to move to a position of statistical significance requires time and volume. If you have a test that isn’t reaching significance, you can think about increasing the traffic to that treatment.
Good article, Jason. Neat.
Good article.
But, I dont think you can reach a higher level of significance by running the test for more days.
It all depends on the data you get. I mean, even after running it for more days, lets say the t-statistic comes out to be the same still, there’s nothing much statistics can do it.
Love the article – my team has been investigating this very math as we are noticing some disturbing issues with our T&T confidence intervals.
Specifically – can you explain how the LIFT confidence intervals are reported? ie. if it’s showing a mean lift of 3% but the little hover option is showing -2% to 8% – how are they getting the -2% – 8% range? From our calcuations, they are taking the test group high bound less control group low bound for the high end and the opposite for the low end.
But – how exactly is that statistical confidence? I need to be able to say “We are seeing a 3% lift +/- X with 95% confidence (or whatever). Question is – how do we get to 3% +/- X% using T&T’s data? Right now, we are forced to calculate outside of T&T using daily aggregates – not ideal. But T&T’s lift intervals are just too wide and do not seem representative of the true error of the lift.
Hi Jason,
I think we can both benefit from talking to each other. Nice post. I’m not on board with how you come to “confidence”, but everyone’s got a different angle.
Cheers,
Jorge
Hi Jorge,
Thanks for the comment. To be clear, this isn’t my methodology. This is the underlying set of calculations that Omniture Test & Target uses within their reporting interface.
Very helpful post–thanks. Glad I came upon your site.
I agree with your reply to Whitney–to increase confidence (and statistical power), you need to increase the sample size.
–Jeff
Thanks for putting this up. I definitely needed a refresher!
The way variance was written tripped me up at first though.
Variance (control) = 9.41(1 – 9.41) = 0.09
would probably be more clearly (and accurately) written as
Variance (control) = .0941(1 – .0941) = 0.09
Otherwise, I think I could easily provide this info in a group setting to a varied group which I think makes it very valuable!
Thanks
Thank you Ty. Sorry for the confusion, I have updated the post. Nice catch.
Sorry about the late comment, but just discovered your blog…
Love worked examples like this, but I would just point that you are starting off with a binomial distribution (conversion rate) but then use a normal distribution for some other calculations (T-Test and confidence intervals). This is totally fine as the normal distribution does approximate the binomial for large number of trials and conversion rates that are not too close to 0 or 1.
The takeaway is just that you should not jump to conclusions about the control and alternative until you have a decent number of trials.
Hi Jason,
Great page, but I found myself totally lost right at the point all the reading through formulas was supposed to pay off! I’m trying to find a way to estimate how many Visitors I’ll need to get significant results if the trends from the last two months continue – that is, I have lots of data, but no clear winner between a couple of different experiences.
Can anyone spell out for me what this last formula is saying:
Student’s T-Test = 1 – TDIST(ABS(0.84),(4003 + 4008 -2),2) = 0.60
?
Is there any way to say (sticking with your example) if the CR’s stay at approximately the same level they have been, how many visits would one need to be confident in the differences that one is seeing?
Thanks for any pointers.
Tom
Hi Tom,
I built the Test Confidence Calculator to do just that. You an plug in your numbers and run “what if” type analysis to determine what kind of volume and CR you need to reach statistical significance. http://www.keystonesolutions.com/community/2011/05/optimization-test-confidence-calculator/
Hope you find this helpful.
-jason